Design Google Search

Google 作为搜索引擎的标杆，帮助用户发现了互联网上无数的精彩。因为有了搜索引擎，在网上找到自己想要查询的信息变得简单快捷。今天我们就一起深挖小小的搜索框是如何帮我们从茫茫互联网上找到内容的。

在系统设计面试中，本题着重考察同学对信息索引 (Index) 和查询 (Query) 的理解。由于搜索引擎数十年的发展，两者概念上的掌握已经不足以应对面试的难度，然而两者优化路径的权衡才是面试的核心考点。

类似的考题有搜索 Wikipedia。

1. 理解需求

1.1 商业目的

让用户可以通过在搜索引擎中键入关键词方便快速及时地找到相关的信息。

1.2 功能性需求

互联网内容会产生变化，需要持续更新索引
搜索单一关键词
搜索多个关键词
搜索关键词组（使用引号表达只搜索数个连续的关键词）

1.3 非功能性需求

时效性 (Time-sensitive) - 对重要网站更新在短时间内更新索引并允许用户搜索
扩展性 (Scalability) - 索引全互联网并支持大量用户搜索
准确性 (Accuracy) - 返回内容与关键词有高相关性
延迟 (Latency) - 用户发出搜索请求之后，在半秒内返回结果

1.4 不需要支持的功能

爬虫 (crawler)
除英语以外的多语言支持
搜索结果排序

2. 资源估算

2.1 假设

互联网上有 500M 网站
平均每个网站100个页面
每个页面 100KB (HTML, JS)
每天有 1B 搜索引擎用户
平均每个用户进行 10 次搜索

2.2 估算

网页存储 - 500M * 100 * 100KB = 5 PB
索引存储 - 跟网页存储在同一个数量级约等于 10 PB
QPS - 1B * 10 / (24 * 3600) = 115741 QPS

3. High-level Diagram

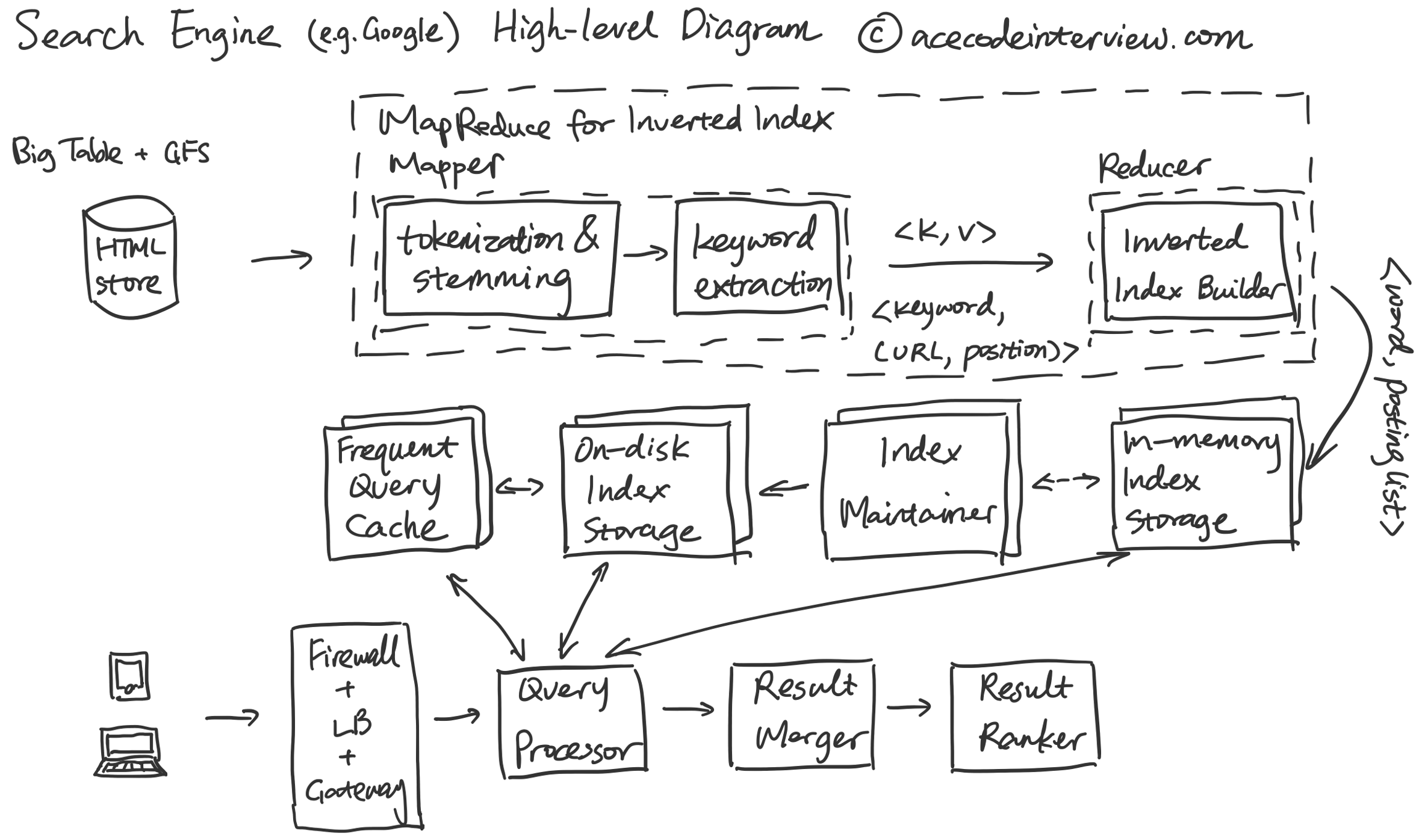
4. 核心子服务设计

搜索引擎设计的重点是支持索引 (Index) 和查询 (Query)。为了更细致地将索引讲清楚，我们进一步把它分成编制索引 (Indexing) 和维护索引 (Index Maintainence)。

4.1 编制索引 (Indexing)

4.1.1 为什么需要索引？

用户会提供给搜素引擎几个关键词，搜索引擎需要从整个公开互联网的内容里找到还有这几个制定关键词的网页。

如果我们不使用索引，那么我们就要在每一次搜索请求之后遍历这个互联网寻找网页，这显然是不能满足延迟要求的。

4.1.2 索引的数据结构

我们可以考虑两种数据结构来存储索引。

使用一个矩阵，X轴是需要检索的文本编号，Y轴是关键词。矩阵里的每个格子有一个 Boolean 表示该关键词是否在文本中出现。
使用一个字典，键是关键词，值是一个链表，包含所有该关键词出现过的文本编号。

从这两个方案中，我们可以观察到方案一所需要的数据存储量远大于方案二，因为方案一的矩阵中大多数格子都是 FALSE，只有少数是 TRUE，非常稀疏 (Sparse)，而方案二的字典能够非常密集 (Dense) 地表达需要包含的信息。

4.1.3 如何编制索引？

编制索引简单来说有几个步骤。

标识化 (Tokenization) - 将文章中的词提取出来
标准化 (Normalization)，词干提取 (Stemming) 和词形还原 (Lemmatization) - 对词进行调整变成语义准确的标准词
对于每篇文章的每个标准词进行逆向索引

其中标识化最简单的形式是将英文语句去除标点符号，按照空格分隔开。这样可以解决多数情况，但仍存在不少问题：

姓名 (e.g. Michael Jordan)
带标点的词 (e.g. o’clock)
约定俗成的词组 (e.g. New York)
停用词 (Stop Word) 也就是过于常见的单词 (e.g. a, an, the)
有特定指代的符号 (e.g. M*A*S*H)
结构性的符号 (e.g. #yolo)
邮箱 (e.g. acecodeinterview@gmail.com)
网站 (e.g. acecodeinterview.com)

其中我们需要对这些不同情况做特殊处理，比如跳过停用词，提取结构性符号的含义，把链接认为是一个单一词等等。

4.1.4 支持词组搜索

用户时常明确地或是不明确的地在搜索框中打入词组，并期待这个词组作为一个整体对待，比如之前提到的 New York。用户并不会认为一篇开头提到了 New 末尾提到了 York 的文章是想要的结果。这时候我们有两种方案。

方案一在编制索引时加入在文章中的位置信息 (positional indexing)
方案二对特定词组进行单独索引 (biword indexing)

方案一的好处是灵活，对于两个甚至更多的词组查询都可以准确给出结果；坏处是查询更慢。

方案二的好处是查询更快；坏处是如果对于任意两个或多个连续单词都认为是词组索引会导致索引大到无可接受。

在权衡利弊之后，我们一般选择以方案一为主，牺牲查询速度，获得灵活性和适当大小的索引。我们仍可以结合方案二，对于部分常用词组，人名等等进行额外的索引，提高查询速度。这种混合策略在保证了灵活性的同时，尤其对常见单词组成的词组 (e.g. 著名英剧 Doctor Who) 有极大的加速效果。

4.1.5 分布式索引编制

为了支持互联网的索引编制，我们无法仅仅使用单一机器而是需要使用分布式的索引编制方法。MapReduce 作为大数据处理的经典框架，在设计之初就把索引作为主要的应用的场景，在这里使用再合适不过。

MapReduce 将计算分成两个步骤，Map 和 Reduce，由多台 Mapper 和 Reducer 完成。MapReduce Workflow - Enrique Alfonseca. (2013). MapReduce for Indexing P5

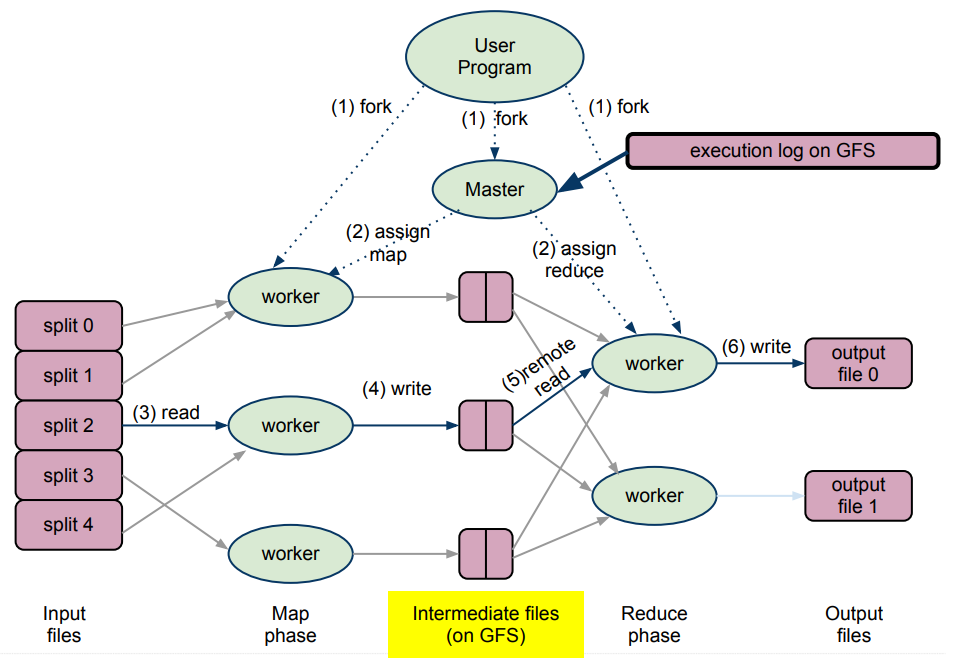
结合之前小节所提到的编制索引的步骤，我们可以这样拆分 Mapper 和 Reducer 的工作。

Mapper - 标识化，标准化，词干提取，词形还原，并且返回一组包含关键词，内容编号和位置信息的键值对 (word, <URL_id, position>)。
Reducer - 每个 Reducer 负责一定范围的关键词，它从中间存储中读取众多 Mapper 对于特定关键词的键值对，并将它们排序合并成一组新的键值对 (word, String(Array[<URL_id, position>])) 写入输出文件，其中的值被称为 Postings List。Postings List 的排序先按照 URL_id，再按照位置。

MapReduce Indexing Code - Enrique Alfonseca. (2013). MapReduce for Indexing P40

4.2 维护索引 (Index Maintenance)

4.2.1 内存和硬盘中的索引

在索引编制完成之后，我们最重要的权衡就是看索引是应该存储在内存还是硬盘中。

首先我们考虑使用内存存储索引，这样做的好处是查询速度快，缺点是昂贵。事实上，Google 这样的大型搜索引擎的大多数索引都是存在内存中的。Term-based vs. Document-based Partition - Justin Zobel, Alistair Moffat. (2006). Inverted Files for Text Search Engines P18

内存中的分布式索引在查询过程中可以根据内容来分区 (Document-based Partition)。处理查询请求的 Master 会将查询分发到存储着不同内容索引的机器上并在每一台机器上生成搜索结果，再由 Master 合并排序。在这里我们不会考虑按照词条分区 (Term-based Partition)，主要原因是部分常用词的 Posting List 无法存入单机的内存。

其次我们考虑使用硬盘存储索引，硬盘相对于内存会有很大的成本节约，如果我们能够降低硬盘的随机读取次数，我们还是可以将延迟控制在一定范围内。这时候，我们可以考虑按照词条分区 (Term-based Partition)，这样对于每一个关键词，我们只需要对硬盘做一次随机访问 (Random Access) 而硬盘的空间也足够大，可以支撑常见词的 Posting List。

SSD 也是值得考虑的第三种方案，SSD 的随机访问和顺序访问的速度接近，可以当做空间更大的内存考虑。Memory-based vs Disk-based Index - Abhishek Das, Ankit Jain. (2012). Indexing The World Wide Web: The Journey So Far P11

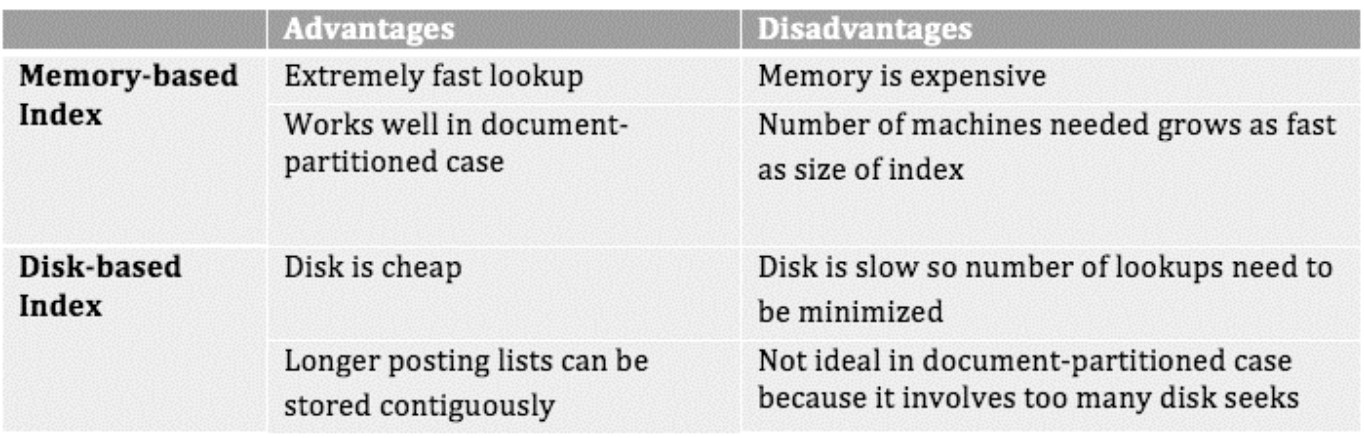
权衡利弊之后，我们倾向于采用 Document-based Partition 加上内存硬盘混合的策略。一方面，在多数情况下，对于常用的索引，也就是每个关键词中排序最靠前的内容的 Posting List（可以是词频最高，也可以是所在网站权重更高），我们保留一定数量的在内存中。另一方面，对于很少被查询的内容，我们可以将这些 Posting List 放在硬盘中，在少数情况下使用。

4.2.2 更新索引

由于索引时常需要更新，我们需要考虑如何将最新检索完毕的索引加入到现有的索引中。

对于内存中的索引，我们需要权衡两种数据结构，Singly Linked List 以及 Variable Length Array。前者插入操作更快速，后者省去了存储指针的空间，同时读取时 CPU 时间花费更少。权衡利弊之后，我们可以选取一条中间道路，Linked List of Fixed-size Array，通过调整数组的大小，我们使得内存中的索引兼具两种数据结构的优点和最小化缺点。

对于硬盘中的索引，就像 4.2.1 中提到的那样，我们的首要目标是减少硬盘随机读取次数。最好的情况下，我们把每个关键词的所有的 Posting List 放在连续的硬盘空间中。下面我们分析一下我们怎么实现这个效果。我们有以下几个选择：重建 (Rebuild)，间歇性合并 (Intermittent Merge)，渐进更新 (Incremental Update)。

重建 - 这个很简单，我们将所有爬取的最新网页重新进行一次检索，用新的索引替代旧的索引。这只适用于小型的检索任务，对于全互联网检索是不合适的。
间歇性合并 - 核心思想是将新生成的索引保存在内存中，在达到一定的空间大小之后一次性跟原有索引合并，生成新索引，并替代原有索引。每一次查询发生时，同时访问内存和硬盘中的索引，让用户可以得到最新的搜索结果。在合并索引的过程中，新的索引不覆盖老索引，而是在硬盘中找到新的一段连续空间。这样，即使在合并索引的过程中，查询依然不会受影响。
渐进更新 - 核心思想是在恰当的时机（内存中的索引达到一定大小或是用户刚查询过该关键词），更新硬盘中特定关键词的 Posting List，这个更新可以是在原有的硬盘空间上，也可以在空间不足时写到新的硬盘空间中。与间歇性合并的区别有两点：第一是渐进更新可以对单一关键词更新，第二是渐进更新写入硬盘的时候可能在硬盘中原有位置更新。

考虑到我们检索全互联网的需求，重建首先排除。后两者中间歇性合并更优，由于硬盘空间相对便宜，在产生新索引过程中暂时存在两份索引最多使硬盘需求翻倍，在可接受的范围内；另外每次重新将索引写入连续的硬盘空间可以保证一次的硬盘随机读取，保证查询速度。

间歇性合并也存在一些问题，就是我们每次更新时总是需要将某个关键词的全部的 Posting List 重写。其实我们不必如此。对于不同更新频率的网站，我们的爬取频率和索引频率是不同的。我们可以将网站按照更新频率分成几个级别。对于不同的级别我们分别编制索引，产生独立的 Posting List。这样我们就可以对经常变化大的网站索引频繁更新的同时，不浪费资源去编写并不更新的网站的索引了。

4.2.3 压缩索引

前面的小节中我们提到了在硬盘中更新索引的方法，但是略过了硬盘中索引的数据结构，这一小节我们就展开讨论。

我们回忆一下之前提到的 Posting List 的数据结构:

关键词：(文档编号1，位置）->（文档编号2，位置）-> ....

最简单的方案是将内存中索引的数据结构序列化 (Serialize) 写入连续的硬盘内存空间里。因为存储索引需要大量的硬盘空间以及相应的缓存空间，在优化思路上我们可以考虑对 Posting List 占用的空间做一些压缩处理。

不记录文档编号的绝对值，只记录文档编号与前一个文档编号的差值。由于我们不需要随机读取 Posting List 的某个位置，而是把它当做一个整体读取，这样只记录差值不会让我们做没必要的读取，同时能够让我们用更小的数字去替代更大的数字。更小的数字可以用更少的比特来存储从而达到压缩的目的。这个方法同样可以使用在文档的位置编号上。
Variable Byte Encoding - 对于不同大小的数字按照需要采用不同数量的比特来代表。实现方法上是每个 Byte 中就有一个 Bit 来表达这个数字是不是最后一位，这样小的数字一个 Byte 可以表达，大的数字可以用多个。

以上的方法不仅可以使占用的硬盘空间减小，更可以减少硬盘到内存的数据传输时间，在实际操作中这个数据传输时间的减少会超过数据解压缩造成的时间增加，使得端到端的速度更快。

4.2.4 优化索引

到目前为止我们讨论的索引还局限在将 Posting List 按照文档编号来排序 (Document-sorted)。我们有没有更优的方法去做排序呢？

下面我们来考虑两种额外的选择：

按照词频来排序 (Frequency-sorted) - 如果一个文档中某一个关键词出现的频率很高，这个文档应该被优先读取。
按照影响力排序 (Impacted-sorted) - 某一个文档可能属于知名的网站，有一些可能属于无名小站，应该优先选择更有更有影响力的网站的文档。

按照这个思路思考下去，我们可以结合多种排序考虑来给 Posting List 设置一个相对复杂的排序算法来让用户在搜索时只需要读取 Posting List 的一小部分就能得到满意的结果。

在有了优化的索引后，我们可以借这个机会优化一下 Posting List 的存储。我们可以将 Posting List 分成一个一个 Block，每次查询时我们尽量在有限的时间内读取最多的 Posting List Block，而不追求将 Posting List 读完。

4.3 查询 (Query)

在了解了索引是如何编制和存储之后，查询的实现就很容易理解了。

4.3.1 单一关键词查询

在查询时，我们会访问以下信息：

关键词查询结果的缓存
内存中的最新索引
硬盘中索引常用 Block 的缓存
硬盘中的索引

我们将这些信息汇总起来进行合并操作，产生该关键词的 Posting List。这个 Posting List 中的相关网站会根据词频，网站权威性等因素进行一次排序 (Rank)，转化为最终用户看到的搜索结果。

4.3.2 多个关键词查询

在单一关键词查询的基础上，我们需要收集多个关键词的 Posting List。我们对这些 Posting List 需要找到一个交集，即我们找寻的网址需要包含所有的关键词。

在文档编号排序的索引情况下，这时候我们可以使用一个简单的算法：在每一个关键词的 Posting List 开头放一个指针，如果遇到同一个文档编号就一起前进，反之，就让更低编号的指针前进。这样就可以在线性时间内找到所有包含所有关键词的网址了。Skip List - Wikipedia

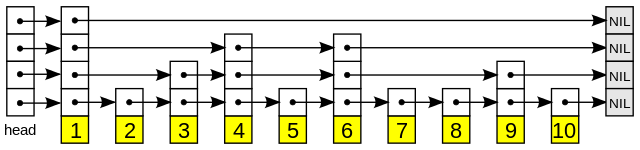
在此基础上，可以使用 Skip List 让我们在低于线性时间 (Sub-linear Time) 内找到想要的结果。Skip List 引入额外的指针跳过数个文档指向更远的文档，这样我们在前进指针的时候同时查询下一个文档和更远的文档，如果更远的文档编号仍小于其他指针对应的文档编号，那么我们就可以直接将指针移到更远的文档上。

4.3.3 关键词组查询

这里的关键词组查询特指要求得到包含完整连续的关键词组的搜索结果。我们可以结合之前提到的两种方法来得到搜索结果。